Researchers from Beihang University and East China Normal University are advancing the field of graph deep learning by integrating concepts from Riemannian geometry, a branch of mathematics focused on curved spaces. The collaborative work by Li Sun, Qiqi Wan, Suyang Zhou, Zhenhao Huang from North China Electric Power University, and Philip S. Yu presents a compelling case that current graph representation techniques often overlook the complex, non-Euclidean structures of graph data. By proposing a framework that utilizes Riemannian geometry, the researchers aim to enhance the effectiveness of graph neural networks, enabling them to better capture the intricacies of relationships between data points.
This study highlights the limitations of traditional methods that treat graphs as existing solely within flat, Euclidean spaces. Instead, the authors argue for a shift towards modeling graphs as residing on Riemannian manifolds—geometric constructs that more accurately reflect the complexity of real-world data. “The intrinsic structure of graphs is often lost when forced into higher-dimensional Euclidean spaces,” said Sun. This perspective is particularly significant given that many existing methodologies focus narrowly on specific manifold types, predominantly hyperbolic spaces, which may not encompass the full diversity of graph structures encountered in practice.
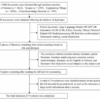
To bridge this gap, the researchers advocate for an intrinsic approach to graph neural network design. This entails a move away from simply embedding graphs into predefined manifolds towards directly modeling their geometry within curved spaces. This foundational shift not only addresses theoretical shortcomings but also proposes a structured research agenda aimed at exploring various manifold types, neural architectures, and learning paradigms. The authors categorize existing techniques across eight representative manifolds, including hyperbolic, spherical, and pseudo-Riemannian spaces, and review six neural architectures such as graph convolution networks and transformers.
“This work is not just about applying Riemannian geometry; it’s about embedding graph neural networks within these intrinsic manifold structures,” stated Wan. By examining how different geometrical assumptions affect model performance, the study provides a useful taxonomy that can guide future research. The emphasis on intrinsic formulations is a crucial aspect, as extrinsic approaches risk missing valuable geometric information by embedding graphs within higher-dimensional spaces.
The findings underline the necessity for a paradigm shift in how scientists perceive graphs within the context of machine learning. Historically, these networks have been treated as flat, abstract constructs, limiting the ability to model complex relationships accurately. “Graphs are inherently geometric objects deserving more focused attention,” Zhou noted, adding that a deeper understanding of their intrinsic dimensionality can lead to substantial improvements in data analysis.
The potential applications of this research are wide-ranging, spanning from recommender systems and social media analysis to molecular biology and physical interaction systems. By framing Riemannian geometry as a foundational principle for graph representation learning, the researchers open avenues for more accurate and insightful data analytics. The authors point out that while current efforts have emphasized hyperbolic spaces, real-world graphs often feature greater complexity, calling for a broader investigation of manifold types.
As this research evolves, it highlights the importance of developing robust theoretical foundations and scalable algorithms to fully realize the potential of Riemannian graph learning. The intersection of these geometric insights with emerging techniques, such as diffusion models, could pave the way for groundbreaking advancements in generative modeling and anomaly detection across complex networks. Ultimately, this work not only seeks to improve algorithms but also aims to enrich our understanding of data itself, marking a significant step forward in the ongoing evolution of graph deep learning.
See also
AI Study Reveals Generated Faces Indistinguishable from Real Photos, Erodes Trust in Visual Media
Gen AI Revolutionizes Market Research, Transforming $140B Industry Dynamics
Researchers Unlock Light-Based AI Operations for Significant Energy Efficiency Gains
Tempus AI Reports $334M Earnings Surge, Unveils Lymphoma Research Partnership
Iaroslav Argunov Reveals Big Data Methodology Boosting Construction Profits by Billions
